Part 1

In Day 7, we are presented with a problem that concerns bags and luggage. We are told that bags are color-coded and must contain specific quantities of other bags. For example, we are given the input data below:

light red bags contain 1 bright white bag, 2 muted yellow bags.
dark orange bags contain 3 bright white bags, 4 muted yellow bags.
bright white bags contain 1 shiny gold bag.
muted yellow bags contain 2 shiny gold bags, 9 faded blue bags.
shiny gold bags contain 1 dark olive bag, 2 vibrant plum bags.
dark olive bags contain 3 faded blue bags, 4 dotted black bags.
vibrant plum bags contain 5 faded blue bags, 6 dotted black bags.
faded blue bags contain no other bags.
dotted black bags contain no other bags.

It turns out that we have a shiny gold bag. The question that we are asked is the following: How many different bag colors would be valid for the outermost bag (i.e., how many bags can countain eventually at least one shiny gold bag)?

At first sight, this problem can seem puzzling. We can see that there are several levels of “layers” of bags that can eventually contain a shiny gold bag. This can be represented with the following graph:

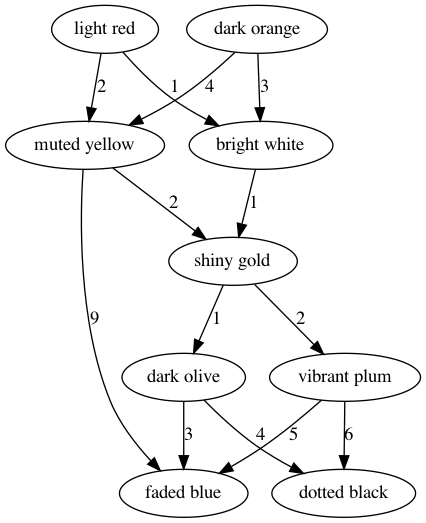
In particlar, we can see that there are in the end four colours that can eventually contain a shiny gold bag: light red, dark orange, muted yellow, and bright white bags. If you are having difficulties seeing this, you can follow these steps:

1. Locate where the shiny gold bag is. It is quite conveniently placed in the middle of the figure;
2. Locate the bags that have arrows that point to the shiny gold bag. In our case, these are muted yellow and bright white bags.
3. Locate the bags that have arrows that point to the muted yellow and bright white bags. In our case, these are light red and dark orange bags.
4. There are no more arrows that point towards these final two bags. And so we have found our final result.

Graphs are also a very important data structures that can model lots of problems. This is not supposed to be a lecture on graphs, but you should at least know that a graph is composed of nodes and edges. There are several ways to represent a graph programmatically, and in this case, I will use a map where keys are going to represent “containers” and values “contents”. For example, we can represent this graph in Python with the following code:

# I'm not representing the 'weights' of each edge for simplicity reasons
bags_map = {
    "light red": ("muted yellow", "bright white"),
    "dark orange": ("muted yellow", "bright white"),
    "muted yellow": ("faded blue", "shiny gold"),
    "bright white": ("shiny gold"),
    "shiny gold": ("dark olive", "vibrant plum"),
    "dark olive": ("faded blue", "dotted black"),
    "vibrant plum": ("faded blue", "dotted blag"),
    "faded blue": (),
    "dotted black": ()
}

This tree already helps us a lot to figure out a solution. But actually, we can represent this data in another format which will help us solve this problem more easily. And that format is simply to reverse the edges, so that we have (content, containers) couples in the map instead of (container, content). We obtain the following graph:

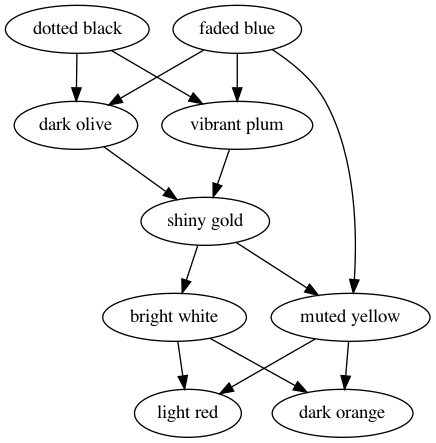
And the corresponding Python representation:

# I'm not representing the 'weights' of each edge for simplicity reasons
bags_map = {
    "light red": (),
    "dark orange": (),
    "muted yellow": ("light red", "dark orange"),
    "bright white": ("light red", "dark orange"),
    "shiny gold": ("bright white", "muted yellow"),
    "dark olive": ("shiny gold"),
    "vibrant plum": ("shiny gold"),
    "faded blue": ("dark olive", "vibrant plum"),
    "dotted black": ("dark olive", "vibrant plum")
}

Let’s see how we can parse the input to produce such a map.

# Because we are "inversing" the graph compared to the input, we can create the
# map in two passes: first to create a set of bags, and second to create the
# actual map.

bags = set()
for line in lines:
    bags.add(line.split(" contain ")[0])

bags_map = {}
for bag in bags:
    containers = set()
    for line in lines:
        # We remove also remove the plural 's' for each container
        # For example, line == "bright white bags contain 1 shiny gold bag."
        container = line.split(" contain ")[0][:-1]
        contents = line.split(" contain ")[1]
        if bag in contents:
            containers.add(container)
    bags_map[bag] = containers

Now, it is just a matter of traversing the graph starting from the shiny gold node. Two common algorithms to do just that are the breadth-first search of depth-first search. For this problem, we are going to implement a breadth-first search (BFS) which is done like this in Python:

# bags_searched is a set of bags we have seen with the BFS algorithm
# bags_queued is the list of bags whose containers still need to be searched
def search_bags(bags_searched, bags_queued, bags_map, current_bag):
    if current_bag != "shiny gold bag":
        bags_searched.add(current_bag)
    bags_queued.append(current_bag)
    while bags_queues:
        bag = bags_queued.pop(0)
        if bags_map[bag]:
            for container in bags_map[bag]:
                bags_searched.add(container)
                bags_queued.append(container)

Part 2

In Part 2, we are asked to compute the number of bags that we are taking with us if we are carrying a single shiny gold bag. In the previous example, we know that:

• A shiny gold bag contains a dark olive bag and two vibrant plum bags;
• A dark olive bag contains three faded blue bags and four dotted black bags;
• A vibrant plum bag contains five faded blue bags and six dotted black bags.

And so, in total, a shiny gold bag contains in total 32 bags in this small example.

Something that we realize here is that the data structure we used in Part 1 is not going to help us a lot in Part 2 (this seems to be a trend in the Advent of Code series). We are still representing the data with a graph, but we need to add in the weights this time. So a possible way of representing the data could be the following:

bags_map = {
    "light red": [(2, "muted yellow"), (1, "bright white")],
    "dark orange": [(4, "muted yellow"), (3, "bright white")],
    "muted yellow": [(9, "faded blue"), (2, "shiny gold")],
    "bright white": [(1, "shiny gold")],
    "shiny gold": [(1, "dark olive"), (2, "vibrant plum")],
    "dark olive": [(3, "faded blue"), (4, "dotted black")],
    "vibrant plum": [(5, "faded blue"), (6, "dotted blag")],
    "faded blue": [],
    "dotted black": []
}

The algorithm to parse the input data thus needs to be adapted to create this dictionary. An aspect we did not really mention earlier is that we need to be careful about how we label each bag. Indeed, bags are sometimes singular, sometimes plural. My solution will create a dictionary where keys have the following format: colour bag (note the singular). What I’ve done might not be the prettiest thing, but it does the trick. Note that I’m also using a defaultdict which needs to be imported from collections. A defaultdict allows to quite simply create dictionaries where values are list thanks to an .append() method.

from collections import defaultdict

bags_map = defaultdict()
for line in lines:
    splitted_line = line.split(" contain ")
    container, contents = splitted_line[0][:-1], splitted_line[1]
    if contents == "no other bags.":
        bags_map[container] = []
    else:
        bags = contents.split(", ")
        for bag in bags:
            # We remove the trailing '.' if necessary
            bag = bag[:-1] if bag[-1] == "." else bag
            # We remove the trailing 's' of the plural form
            bag = bag[:-1] if bag[-1] == "s" else bag
            # We take advantage of noticing that a bag can never contain more
            # than a single-digit number of another bag.
            # We also remove the whitespace between the digit and the bag.
            dict_value = int(bag[0]), bag[2:]
            d[container].append(dict_value)

Now, with such a list, we have to compute the number of bags that a shiny gold bag contains. We can do this recursively and that should solve our problem:

def count_bags(bags_dict, bag):
    # If the bag cannot contain any other bag
    if not bags_dict[bag]:
        return 1
    count = 0
    for (quantity, content) in bags_dict[bag]:
        # If a bag contains some other bags, we first add these ones before
        # adding the contents times the quantity of the container.
        if bags_dict[bag]:
            count += quantity
        count += quantity * count_bags(bags_dict, content)
    return count

Concepts and difficulties

Day 7 has a very interesting set of problems as they require us to represent our data in different forms.

The main concept at play here concerns graphs, which are data structures that are quite commonly used to represent complex real life data (just think about social networks). There are lots of ways we can represent a graph, the main ones being: adjacency lists, adjacency matrices, list of nodes and edges, or dictionaries. In this set of problems, we have used dictionaries to represent the input data and work our solution.

Working with graphs is difficult, but that’s also because graphs can represent data that is much more complex than the data structures we have seen since Day 1. It’s important to think beforehand about how the data is going to get represented, because that can really change the complexity of your solution (as illustrated in Part 1). I think these exercices could be very well used in practice sessions on graphs if students already have a strong algorithmic background.