Part 1

Day 10’s problem is about charging outlets and adapters. We wish to charge some device, and we need to make sure that we use each end every adapter to charge it. There are, however, additional rules:

• Each adapter must be use at most once;
• The “joltage” difference between two adapters must be at most 3.
• The first charging outlet has an effective joltage of 0.
• Our device has a built-in joltage adapter 3 jolts higher than the highest-rated adapter we have.

We are then given a list of joltage ratings for our adapters, and the question in Part 1 is to compute the product of the number of 1-jolt differences and the number of 3-jolt differences.

16
10
15
5
1
11
7
19
6
12
4

One thing that is actually quite straightforward is that, because we have to use all the adapters, we can simply sort these by increasing joltage to get the actual sequence of adapters being plugged one after the other. Then, it’s just a matter of counting the 1-jolt or 3-jolt differences. We simple need to be careful and remember about the charging outlet (which has a joltage of 3) and our device adapter, which is automatically 3 jolts higher than our highest-rated adapter. So, that would give the following program in Python:

adapters = [int(adapter) for adapter in lines]
adapters.sort()

# We take into account the charging outlet, which may produce a 1-jolt difference
off_by_one = 1 if adapters[0] == 1 else 0
# We take into account the device adapter, which produces a 3-jolt difference
off_by_three = 1

for i in range(len(adapters[:-1])):
    if adapters[i] + 1 == adapters[i + 1]:
        off_by_one += 1
    elif adapters[i] + 3 == adapters[i + 1]:
        off_by_three += 1
print(off_by_one * off_by_three)

Part 2

In Part 2, the rules are changing a little bit: while the 1-3 jolt difference still applies, we don’t have to use all the charging adapters anymore. And now, the question we have is: how many distinct arrangements of charging adapters are there?

If we take the example input given a little higher, this is all the arrangements we have following these new rules:

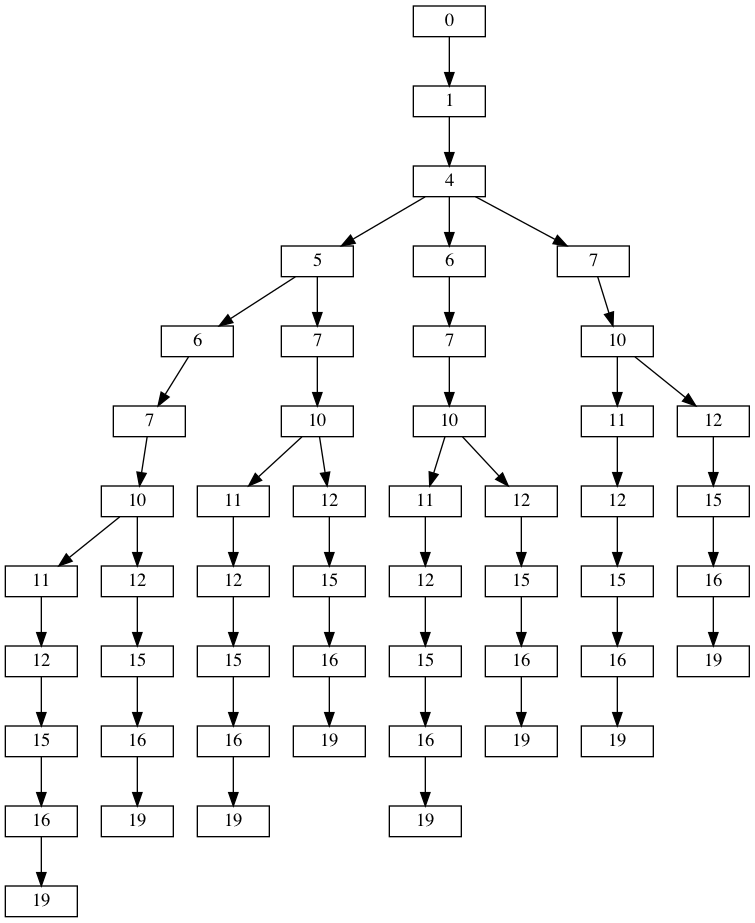
If we simply count the number of leaves on this tree, we find that 8 is the number of distinct arrangements for this input sample. This illustration should also give us some idea on how to solve Part 2: we could create such a tree and recursively check each adapter for its number of possible “sub-adapters”. If we end up on a leaf, we simply return the value 1.

Let’s see how we can create such a tree first. Although I have never mentioned it before, the Python syntactic sugar helps a lot in creating what we want thanks to list comprehension.

# adapters is the sorted list of integers we have created in Part 1
# It's quite easy to create the list of possible values thanks to list comprehensions
tree = {0: [x for x in adapters if x <= 3]}
for i, adapter in enumerate(adapters):
    values = [x for x in adapters[i + 1:] if x - adapter <= 3]
    tree[adapter] = values

Now we can start to think about the recursive function that will count the number of terminaisons in the tree. However, before we do that, there’s a line in the problem statement we haven’t paid attention to yet:

There must be more than a trillion valid ways to arrange them! Surely, there must be an efficient way to count the arrangements.

If we look at the tree illustrated above, we can actually see something: because of how the tree is built, the ends of each branch always have the same nodes. In the illustration above, we see that the arrangements are always the same after node 12. And so, we realize that there is a way to optimize our algorithm a little bit if we were able to “memorise” how each node can terminate. Like this, we would not be recursing again and again in the same nodes. This technique is actually called memoization. It relies on a map that will store the values we want (in our case, the number of branches that stem from each node).

With memoization, Part 2 can be solved pretty quickly (and elegantly).

def memo_search(memo_map, current_node):
    # If the memoization map does not have a value for our current_node
    if current_node not in memo_map.keys():
        # We set it to 1 if it's a leaf
        if not graphe[current_node]:
            memo_map[current_node] = 1
        # We apply the recursive call on each following node
        # with a list comprehension and compute the sum of the list
        else:
            memo_map[current_node] = sum(
                [memo_search(memo_map, node) for node in graphe[current_node]])
    return memo_map[current_node]


# Same part as shown previously
# adapters is the sorted list of integers we have created in Part 1
# It's quite easy to create the list of possible values thanks to list comprehensions
tree = {0: [x for x in adapters if x <= 3]}
for i, adapter in enumerate(adapters):
    values = [x for x in adapters[i + 1:] if x - adapter <= 3]
    tree[adapter] = values
memoization_map = {}
arrangements = memo_search(memoization_map, 0)
print(arrangements)

Concepts and difficulties

Part 1 of Day 10 does not present any sort of difficulty. The only aspect that could trick us is to forget about the first and last joltage difference.

Part 2 is more interesting. It requires that we create a map that would represent the tree of all possibilities. Then, we could creating a simple recursive function, but that would quickly become too time-consuming because there are so many arrangements in the real input data! For example, my final answer is 3,022,415,986,688 (well above 1 trillion, as the problem statement says)! And so, Part 2 is a very good opportunity to showcase the use and interest of memoization, which makes my algorithm produce this results in 458ms.